By http://oasitech.it
Altri appunti su http://www.elettronicamaster.altervista.org
Numerosi articoli di elettronica con progetti tutoria ecc li trovate a questo indirizo(da non perdere):
http://www.oasitech.it/linx
Antenne
By Oasitech http://www.oasitech.it

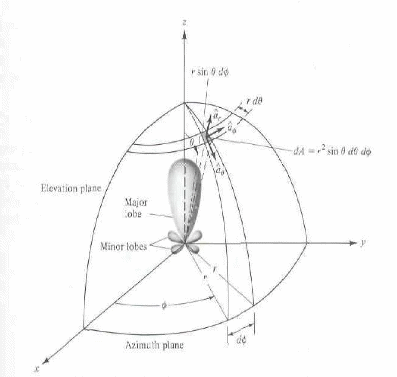
In
un sistema di riferimento sferico![]() con l'antenna centrata nell'origine il campo lontano generato da una
distribuzione di corrente sull'antenna si può scrivere in
termini fasoriali come:
con l'antenna centrata nell'origine il campo lontano generato da una
distribuzione di corrente sull'antenna si può scrivere in
termini fasoriali come:
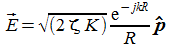
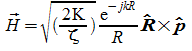
essendo:
K = K(![]() )
la cosiddetta intensità di radiazione dell'antenna, da cui
otteniamo il ben noto diagramma di radiazione
)
la cosiddetta intensità di radiazione dell'antenna, da cui
otteniamo il ben noto diagramma di radiazione
![]() il versore di
polarizzazione del campo elettrico
il versore di
polarizzazione del campo elettrico
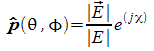
noto a meno di un certo angolo arbitrario. Può essere complesso, ed ha modulo unitario.
![]() l'impedenza
caratteristica del mezzo (il vuoto)
l'impedenza
caratteristica del mezzo (il vuoto)
R: la distanza dal centro del sistema di riferimento sferico al punto dove vogliamo calcolare il campo.
![]() il versore di propagazione radiale, rispetto all'origine del sistema
di riferimento sferico, è diretto radialmente lungo R.
il versore di propagazione radiale, rispetto all'origine del sistema
di riferimento sferico, è diretto radialmente lungo R.
Il
vettore di Poynting risultante dal prodotto tra i due campi elettrico
e magnetico decade come
![]() ed è diretto come il versore di R. E' un'onda sferica quindo
con vettore di Poynting:
ed è diretto come il versore di R. E' un'onda sferica quindo
con vettore di Poynting:
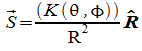
In generale possiamo anche scrivere
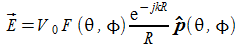
ove V0 rappresenta l'eccitazione della corrente sull'antenna(ha le dimensioni di una tensione) è un numero complesso, e F è un fattore direttamente proporzionale all'intensità di radiazione, che può essere un numero complesso.
Sapendo che il vettore di Poynting è:
![]()
a
grande distanza![]() i
due campi E ed H sono ortogonali e ortogonali anche al versore di
propagazione ed in rapporto sono pari ad H, quindi abbiamo:
i
due campi E ed H sono ortogonali e ortogonali anche al versore di
propagazione ed in rapporto sono pari ad H, quindi abbiamo:
![]()
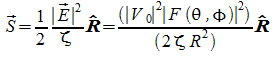
ed otteniamo in pratica la stessa formula di prima dove come si vede F è direttamente proporzionale a K, cioè all'intensità di radiazione.
Vediamo ora come può essere trovata la soluzione dell'equazione di Maxwell che è stata vista in forma generale per alcuni casi pratici.
Dalla teoria della radiazione si ha:
![]()
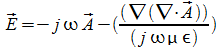
![]()
in cui A è il potenziale vettore, da cui ottenere E ed H.
La soluzione dell'equazione di cui sopra di A da:

ove J è la densità di corrente, sorgente del campo elettromagnetico.
se abbiamo distribuzioni lineari allora
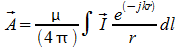
in
campo lontano(zona di fraunhofer)
![]() ove D sono le dimensioni del sistema in esame:
ove D sono le dimensioni del sistema in esame:
![]()
![]()
![]()
![]()
A può essere ottenuto agevolmente in coordinate sferiche e l'espressione di E ed H è immediata
Esempi:
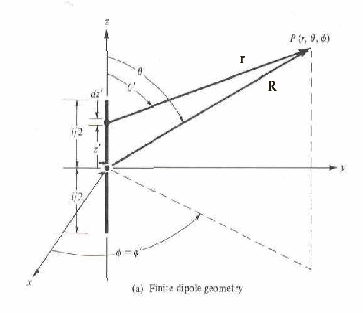
Dipolo Hertziano
![]()
è una corrente cosinusoidale diretta lungo z su un filo di corrente lungo l di lunghezza molto inferiore alla lunghezza d'onda; quindi:
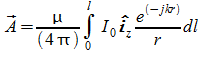
ritendendo r: la lunghezza dell'elemento molto piccolo di corrente dal punto in cui viene calcolato il potenziale vettore, costante e all'incirca la stessa della distanza dal centro del sistema di riferimento(a metà del dipolo stesso) R:
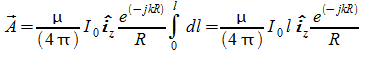
quindi il potenziale vettore è diretto lungo z, le sue componenti lungo un sistema di riferimento sferico sono:
![]()
![]()
![]()
sfruttando
la formula dei campi a grande distanza
![]()
![]()
si ha:
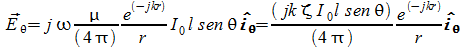
quindi:
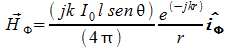
le altre due componenti sono nulle.
Dipolo corto
![]()
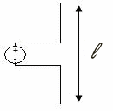
Il dipolo corto può essere interpretato come un filo alimentando a due morsetti di ingresso su due tronchi di una linea di trasmissione. La distribuzione del campo può essere assunta come quella di una linea di trasmissione lunga l/2. Tale lunghezza in questo caso è molto minore della lunghezza d'onda e possiamo per essa quindi prendere la seguente espressione:
![]()
posto che sia z' la cordinata generica lungo un'asse z'. Con (x, y, z) in genere si indica le coordinate di un punto P nello spazio nel quale si vuole trovare il campo.
Ovviamente se vogliamo il campo dobbiamo trovare le formule viste prima, in tal caso come in tutti i casi d'altronde, possiamo integrare ogni contributo elementare sul filo come supponendo costante
su ogni pezzetto dell'antenna ipotizzando che questo irradi la stessa onda irradiata da un dipolo elementare; quindi abbiamo:
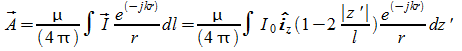
ove r è la distanza del singolo pezzettino di antenna dal punto P come si può vedere in figura:
in
generale
![]() iptizzando
r ed R paralleli
iptizzando
r ed R paralleli
in
tal caso quindi:
![]()
in
zona di Fraunhofer tale approssimazione può essere effettuata
per la fase, mentre per l'ampiezza possiamo usare quella più
grossolana
![]() ,
in tal caso il termine a denominatore può essere portato fuori
dall'integrale. In questo caso poiché la lunghezza
dell'antenna è molto piccola
,
in tal caso il termine a denominatore può essere portato fuori
dall'integrale. In questo caso poiché la lunghezza
dell'antenna è molto piccola
possiamo usarla anche per la fase:
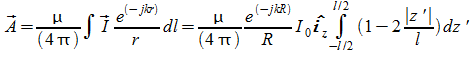
applicando le formule viste prima per il campo otteniamo:
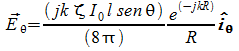
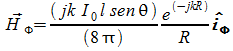
è immediato riferirsi alle grandezza prima citate per la formula generale:
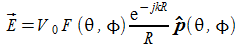

![]()
![]()
nel caso in cui la lunghezza del dipolo divenga confrontabile con la lunghezza d'onda occorre fare un'approssimazione meno grossolana della fase quale quella che abbiamo riportato poco sopra ed integrare rispetto ad essa. L'espressione ovviamente diventa un po' più complicata del caso del dipolo corto.
Dipolo
di lunghezza paragonabile alla lunghezza d'onda
![]()
In tal caso:
![]()
![]()
Ipotizziamo che la corrente sia esprimibile come quella su una linea di trasmissione di lunghezza pari alla metà dell'estensione dell'antenna.
Abbiamo:
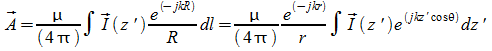
essendo:
![]()
sviluppando e passando all'espressione del campo(i conti sono molto laboriosi) otteniamo:
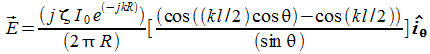
nel
caso di dipolo di lunghezza
![]() si
ha:
si
ha:
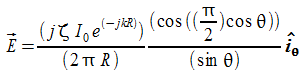
è caratterizzato da un diagramma di radiazione più direttivo del dipolo corto anche se non così efficiente. Tali antenne vengono usate molto spesso nella pratica proprio perchè non particolarmente direttive sono comode ad esempio in diversi casi, quale ad esempio la radiodiffusione. Trattandosi di un sistema di Broadcasting essa deve raggiungere molte utenze e quindi vengono usate tali antenne.
Nel
caso di un dipolo a mezz'onda l'espressione della corrente si può
trovare in maniera abbastanza agevole; la linea ha lunghezza
![]() l'espressione
della corrente per una linea di trasmissione in circuito aperto è:
l'espressione
della corrente per una linea di trasmissione in circuito aperto è:
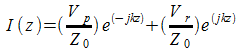
ove Vp e Vr sono i fasori dell'onda progressiva e regressiva sulla linea. Essendo aperta e supponendo che il carico in questo caso infinito sia posizionato in z=0, si ha:
![]()
quindi Vp=Vr. Otteniamo:
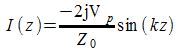
ponendo
z=0 ai morsetti dell'antenna con un'asse z' che va da -l/s a l/2 ed
![]()
![]()
in cui I0 è la corrente massima posizionata proprio sui morsetti dell'antenna. Dall'equazione si vede che la corrente è semplicemente un solo arco di sinusoide lungo tutta l'antenna. In pratica è un onda stazionaria che pulsa con il tempo con la stessa forma:
![]()
per il dipolo a mezz'onda abbiamo il seguente diagramma di radiazione
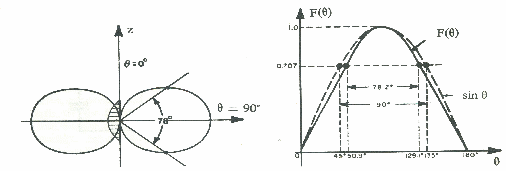
nel
piano equatoriale il diagramma è omnidirezionale, nel piano di
![]() il
diagramma è un po' più direttivo del dipolo Hertziano
con un ampiezza del fascia a metà potenza di 78°, mentre
per il dipolo Hertziano questo vale 90°.
il
diagramma è un po' più direttivo del dipolo Hertziano
con un ampiezza del fascia a metà potenza di 78°, mentre
per il dipolo Hertziano questo vale 90°.
Il campo elettrico può essere polarizzato in diversi modi, ricordiamo al proposito che possiamo avere i seguenti casi: ellittica, circolare, lineare
Ricordiamo che il caso generale è il caso ellittico. Infatti
![]()
avendo
posto:
![]()
il fasore del campo elettrico stesso con ovvia notazione dei simboli; le componenti del campo elettrico danno luogo nella rotazione ad un ellisse. In assenza di componente sinusoidale, cioè solo cosinusoidale avremmo una polarizzazione lineare.
Dal punto di vista fisico il j significa che abbiamo due componenti sfasate di 90°.
In
generale il campo è contenuto in un certo piano, comunque sia
possiamo ipotizzare di prendere due assi lungo il quale il campo ha
due componenti. In coordinate cartesiane possiamo prendere due assi
x,y e quindi due versori
![]()
esempio
consideriamo il fasore:
![]()
si verifica facilmente che in tal caso la polarizzazione è circolare, oltre a questo essa è un'onda piana che si propaga lungo z, questo perchè abbiamo due componenti massime della stessa lugnghezza lungo x e y.
Infatti abbiamo
![]()
poniamo z=0
![]()
per vedere in che verso è la polarizzazione si può guardare due istanti successivi, ad esempio per semplicità t=0 e t=T/4:
![]()
![]()
in un sistema di riferimento cartesiano con una terna x,y,z abbiamo un campo che è polarizzato in maniera destrogira (ossia orario).
Si può vedere facilmente che esso descrive una circonferenza. Infatti, prendiamo e(0;t):
![]()
![]()
quindi:
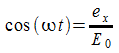
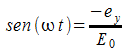
sfruttando la ben nota proprietà delle funzioni trigonometriche:
![]()
abbiamo:
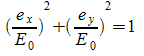 =>
=>
![]()
che è proprio l'equazione di un cerchio di raggio E0.
4. Parametri
Vediamo ora i parametri piu' importanti delle antenne
Direttività

cioè il rapporto tra la densità di potenza a distanza R e la densità di potenza isotropica di un antenna che irradia la stessa potenza alla stessa distanza R.
Su una sfera di raggio R quindi otterrei
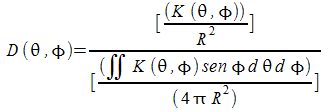
otteniamo
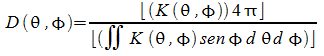
essendo
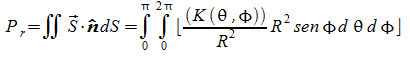
Guadagno
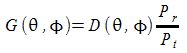
ove con ovvia notazione dei simboli una è la potenza irradiata l'altra la potenza trasmessa (erogata) all'antenna.
Efficienza ohmica
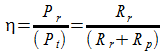
Altezza efficace, h tale che
![]() tensione a vuoto ai
morsetti dell'antenna
tensione a vuoto ai
morsetti dell'antenna
ove Ei è il campo incidente.
Ampiezza del fascio a metà potenza
E' l'angolo di apertura del fascio, i cui due estremi rappresentano i punmti in coordinate sferiche ove il campo decade di 3db.
Area equivalente, tale che:
![]()
ove P è la potenza disponibile ottenuta dal modulo vettore di Poynting moltiplicato con l'area equivalente stessa. E' valida in condizioni di adattamento di massimo trasferimento di potenza e con adattamento di polarizzazione, cioè h ed E paralleli.
Questa formula si può esplicitare meglio considerando
Circuito equivalente dell'antenna in ricezione
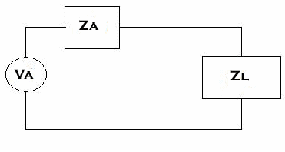
ove:
Va: tensione che si avrebbe a vuoto(ZL infinita) ai morsetti dell'antenna
Za: impedenza dell'antenna
ZL: carico posto a valle dell'antenna(ai suoi morsetti di uscita)
la potenza dissipata sul carico è:
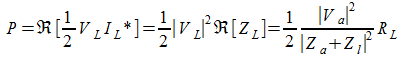
inoltre sapendo che:
![]() supponendo di essere in condizioni di adattamento di impendenza
supponendo di essere in condizioni di adattamento di impendenza
![]()
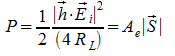
ove
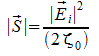
quindi
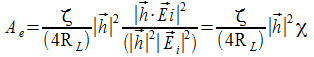
ove
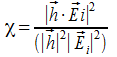 è detto fattore di polarizzazione
è detto fattore di polarizzazione
siccome Ae come detto è definito in condizioni di adattamento di polarizzazioni tale fattore deve essere unitario, quindi:
![]()
ovvero antenna e campo incidente devono dar luogo alla medesima polarizzazione, il coniugato intuitivamente ci dice che questa formula è valida per lo stesso sistema di riferimento, ma un osservatore che vede l'onda incidente è posto dalla parte opposta di un osservatore che vede l'onda generata venirgli incontro.
Vediamo ora una tabella riassuntiva di vari tipi di antenne.
Tabella relativa a vari tipi di antenne
|
Tipo di Antenna |
Diagramma di radiazione |
|
Dipolo Hertziano |
|
|
Dipolo corto |
|
|
Dipolo in mezz'onda
|
|
Queste antenne filari generano un campo scarsamente direttivo. Per ottenere alta direttività si fa uso in genere di antenne ad apertura. Inoltre l'efficienza ohmica è molto bassa essendo bassa la resistenza di radiazione.
Per trovare la resistenza di radiazione si può effettuare il seguente procedimento: calcolare la potenza irradiata a grande distanza ed uguagliarla alla potenza dissipata sulla resistenza di radiazione.
Esempio
Calcoliamo la resistenza di radiazione del dipolo corto.
![]()
sapendo che:
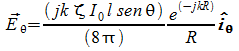
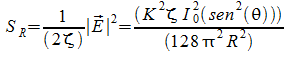
quindi:
![]()
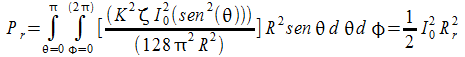
tenendo conto che:
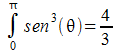
sviluppando si ottiene:
![]()
da cui si
vede che essendo
![]() la
resistenza di radiazione è molto piccola.
la
resistenza di radiazione è molto piccola.
In genere le antenne filari si usano in ricezione per frequenze al di sotto del Ghz, mentre le antenne ad apertura si usano a frequenze elevate f>1Ghz.
Antenna Yagi-Uda
Un caso particolare di antenna interessante, molto usato nella pratica, è quello dell'antenna Yagi-Uda dal nome di due ingegneri giapponesi suoi inventori.
Essa può essere vista come un allineamento di antenne, ma in generale ha un solo dipolo attivo, piu' una serie di elementi parassiti come si può vedere nella seguente figura:
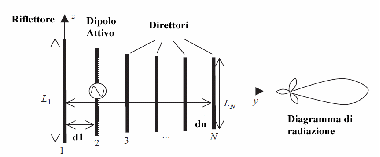
in particolare abbiamo un elemento parassita un po' più lungo immediatamente vicino al dipolo alimentato, il cosiddetto riflettore. E' quest'ultimo in modo particolare insieme al dipolo attivo a determinare il comportamento di quest'antenna rendendolo più direttivo. Più a destra ci sono altri elementi parassiti che generano ulteriore direttività i cosiddetti direttori. Il dipolo attivo genera una certa corrente che si accoppia agli elementi vicini inducendo quindi delle correnti su di essi. Esso può essere costituito da un dipolo a mezz'onda ad esempio; sappiamo che il suo diagramma di radiazione non è particolarmente direttivo, anzi nel piano equatoriale è omnidirezionale, la direttività quindi scaturisce dall'accoppiamento con i dipoli parassiti vicini.
Sapendo che il generico dipolo genera a grande distanza un campo:
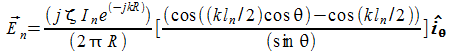
si ha per il campo totale:
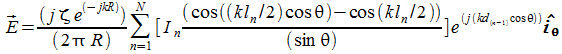
dove dn è la distanza dei singoli dipoli dal direttore posto a una delle estremità dell'antenna.
Variando opportunamente la lunghezza dei singoli elementi e la loro distanza dal dipolo direttore, si può raggiungere il diagramma di radiazione voluto, in particolare variando la lunghezza del dipolo direttore. Nella pratica esso è leggermente più lungo del dipolo attivo mentre i direttori sono leggermente più corti. Il Dipolo attivo accoppiandosi con il riflettore fa si che in determinate direzioni il campo sia in fase mentre in altre in controfase.
Quest'antenna in genere viene usate come antenna ricevente TV nelle abitazioni.
In spazio libero per due antenne in linea di vista (LOS) a distanza d troviamo la potenza ricevuta Pr.
Siano:
Pt: potenza trasmessa(in realtà andrebbe considerata quella effettivamente irradiata, per ipotesi si assume l'efficienza ohmica unitaria).
Gt: guadagno dell'antenna in trasmissione.
Gr: guadagno dell'antenna in ricezione.
Dal momento che nella pratica si usa antenne direttive conviene usare la seguente quantità:
![]() Effective Isotropic
Radiated Power
Effective Isotropic
Radiated Power
con essa si esprime la potenza irradiata a grande distanza da un antenna isotropica equivalente a quella in esame(di trasmissione). La densità spaziale di potenza a distanza d sarà:
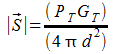
sappiamo che la potenza disponibile ai morsetti dell'antenna vale:
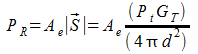
dalla teoria delle antenne usiamo la seguente formula:
![]()
quindi:
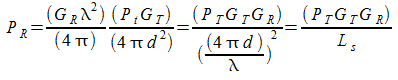 =>
=>
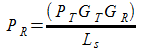 detta Formula di Friis
detta Formula di Friis
avendo espresso Ls: perdita per attenuazione in spazio libero.
Quest'equazione ci dice che ovviamente la potenza in ricezione aumenta se aumenta la potenza con cui si alimenta l'antenna, e se aumentano i guadagni delle due antenne di ricezione e trasmissione. Ovviamente tali guadagni come sappiamo sono correlati alla direttivita e non sono costanti come li abbiamo riportati nella formula. L'equazione di Friis però fa l'ipotesi di considerare i guadagni massimi. Essa diminuisce anche con l'aumentare della perdita per attenuazione in spazio libero Ls; come si vede essa aumenta tanto piu' aumenta la distanza d tra le due antenne come è logico; Ls dipende anche dalla lunghezza d'onda. La perdita aumenta tanto più tale valore diminuisce, cioè la potenza ricevuta tanto maggiore è la frequenza.
In genere non è detto sempre che antenna trasmittente e ricevente si vedano; questo è vero nei ponti radio in genere dove si sfrutta la propagazione troposferica(per diffrazione) e per comunicazioni satellitari. In quest'ultimo caso la distanza viene ad assumere valori molto grandi e quindi la potenza trasmessa deve essere molto elevata. Sul satellite occorrono ampolificatori di potenza che rigenerino il segnale verso terra (es Klystron, Magnetron ecc..).
In molti casi pratici tale equazione non va più bene, un caso tipico è quello di comunicazioni wireless in area urbana dove si ha una condizione NLOS.
6. Circuiti
equivalenti ed adattamento
In trasmissione abbiamo:
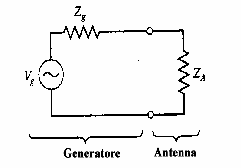
un generatore con la impedenza interna alimenta un antenna vista come un'impedenza Za. Tutta la potenza fornita all'antenna deve essere irradiata in condizioni ideali. Quindi:
![]()
l'impedenza d'antenna è quindi data fondamentalmente da un contributo resistivo sovrapposizione della resistenza di radiazione e della resistenza di perdita responsabile della perdita per effetto juole soll'antenna, e di un contributo reattivo di difficile quantificazione in generale. Nel caso di un dipolo a mezz'onda la parte reattiva tende ad annullarsi rispetto a quanto vede il generatore.
In ricezione abbiamo:
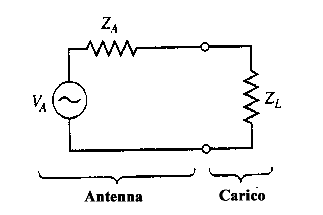
un generatore Va, tensione a vuoto ai morsetti dell'antenna con in serie la stessa Za che alimenta un certo carico. ZL è in pratica la resistenza equivalente vista ai morsetti di uscita dell'antenna del circuito posto a valle della stessa. In casi reali questa può essere la resitenza di ingresso di un preamplificatore a basso rumore.
Adattamento
Nei circuiti delle telecomunicazioni l'adattamento è in generale di due tipi
Adattamento di potenza
Adattamento di uniformità
il
primo fa riferimento al massimo trasferimento di potenza tra
generatore e carico, e si realizza facendo si che il carico del
generatore assuma la seguente espressione:
![]()
mentre per quanto riguarda l'adattamento di uniformità questo fa riferimento al fatto che dal generatore al carico(es antenna) deve essere interposto in genere un cavo coassiale o una guida d'onda. In questi mezzi guidati potrebbe esserci un'onda riflessa che ritorna sul generatore dando luogo a dei picchi di tensione e quindi con possibilità che ci sia un danneggiamento del generatore stesso. Il problema può essere superato interponendo due circuiti tra il generatore e l'antenna nel seguente modo:
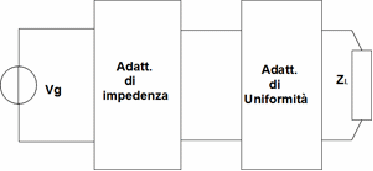
per l'adattamento di uniformità prendendo in esame le formule delle linee di trasmissione:
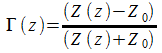 coefficiente di
riflessione
coefficiente di
riflessione
ove
Z(z) e Z0
sono
rispettivamente l'impedenza all'ascissa z della linea e quella
caratteristica della linea di trasmissione; occorre avere un
coefficiente di riflessione nullo. Questo può essere fatto con
i normali metodi delle linee di trasmissione ad esempio facendo uso
di un trasformatore in
![]() posto
in un punto a una certa distanza dal carico nel quale l'impedenza
risulta puramente reale.
posto
in un punto a una certa distanza dal carico nel quale l'impedenza
risulta puramente reale.
Analoghi discorsi possono essere fatti per un'antenna ricevente, in tal caso il generatore è proprio rappresentato dall'antenna e il carico dal preamplificatore.
In molti casi pratici come abbiamo visto per l'antenna Yagi -Uda per conferire direttività al sistema radiante, si può usare un'insieme di antenne. Se il singolo elemento radiante è alimentato questo si dice allineamento di antenne.
Consideriamo il generico campo irradiato da un'antenna a grande distanza:
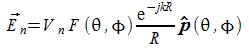
se
abbiamo un allineamento di N antenne allora il campo totale a grande
distanza dal sistema(![]() dove D è la dimensione massima del sistema):
dove D è la dimensione massima del sistema):
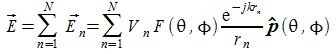
un caso particolare molto interessante è quello in cui il sistema di antenne costituisce un allineamento uniforme di dipoli come nella seguente figura visti dall'alto:
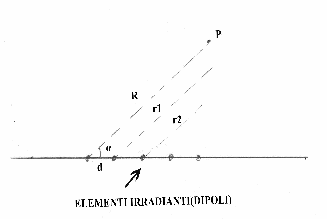
il punto P supponiamo sia posizionato in zona di Fraunhofer e quindi che i raggi che congiungono le antenne con il punto P ove si vuole trovare il campo siano pressochè paralleli.
Le singole distanze delle antenne dal punto in esame si possono esprimere pere la fare al solito come:
![]()
essendo R la distanza del primo dipolo dal punto P, sul quale dipolo abbiamo posizionato il sistema di riferimento.
Abbiamo:
![]()
quindi:
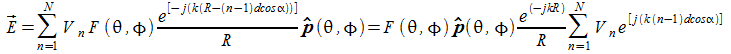
quindi:
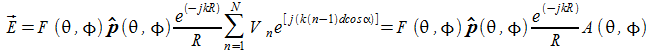
abbiamo il prodotto di due fattori: il diagramma di radiazione del singolo elemento per un altro fattore denominato fattore di schiera. Questo si è fatto ipotizzando che ogni elemento irradi nella stessa maniera e abbia la stessa polarizzazione. Da questo discende la
regola di Krauss: il diagramma di radiazione è il risultato del prodotto del diagramma di radiazione del singolo elemento per il fattore di schiera di una schiera di radiatori isotropici.
Essa discende in pratica dal fatto che visti separatamente essi hanno proprio questo significato dato loro dalla regola di Krauss stessa.
Ipotizziamo per semplicità che
![]()
cioè di prendere le eccitazioni dei singoli dipoli a sfasamento progressivo, supponendo V0 costante.
In questo caso si ha:
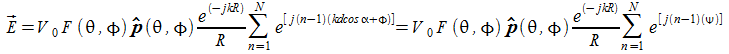
da cui:
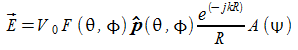
avendo posto:
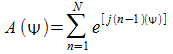 che è il
fattore di schiera ove
che è il
fattore di schiera ove
![]()
è questo termine come ci dice anche la regola di Krauss a conferire direttività alla schiera di antenne. Infatti esplicitando la sommatoria ponendo m=n-1 si ha:
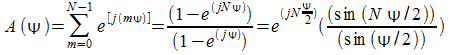
![]() è
una funzione periodica di periodo
è
una funzione periodica di periodo
![]() con
un primo zero in
con
un primo zero in
![]() come si vede nella
seguente figura:
come si vede nella
seguente figura:
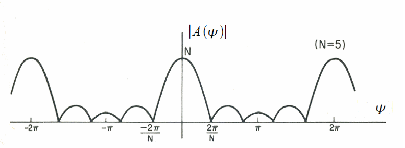
nei dintorni dell'origine esso è quindi tanto più stretto quanto maggiore è il numero degli elementi, ciò significa che il digramma di radiazione diventa tanto più stretto quanto più aumenta il numero degli elementi radianti. Questo però spesso genera dei lobi laterali com e possiamo vedere da alcuni diagrammi riportati per N diverso e a due distanze diverse tre gli elementi:
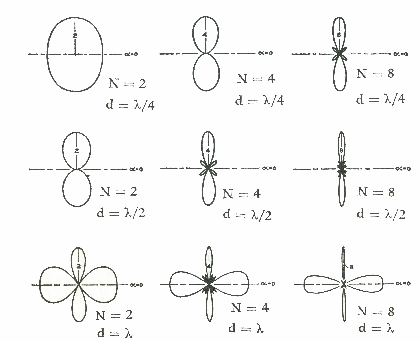
per l'argomento dei seni tendente a zero abbiamo in particolare una sinc:
![]()
il
massimo viene raggiunto in
![]() quindi
quindi
![]()
al
variare di
![]() abbiamo tre casi particolari:
abbiamo tre casi particolari:
Broadside
in
cui
![]() quindi occorre porre
quindi occorre porre
![]()
gli elementi irradiano massimamente in direzione ortogonale alla loro disposizione
Endfire
in
cui
![]() quindi occorre porre
quindi occorre porre
![]()
è il caso in cui gli elementi irradiano massimamente in direzione parallela alla loro disposizione.
Backfire
in
cui
![]() quindi occorre porre
quindi occorre porre
![]()
è il caso in cui gli elementi irradiano massimamente in direzione parallela alla loro disposizione ma in direzione opposta al caso endfire.
Se
invece
![]() non assume uno di questi valori in genere viene chiamato angolo di
scansione. Questo perchè con queste antenne si può
variare elettronicamente tale anmgolo in modo da fargli assumere
qualunque valore e può essere usato ad esempio per scandire
una determinata regione spaziale. Ovviamente questo si fa variando le
fasi con cui si eccita le antenne, in particolar modo variando la
fase
non assume uno di questi valori in genere viene chiamato angolo di
scansione. Questo perchè con queste antenne si può
variare elettronicamente tale anmgolo in modo da fargli assumere
qualunque valore e può essere usato ad esempio per scandire
una determinata regione spaziale. Ovviamente questo si fa variando le
fasi con cui si eccita le antenne, in particolar modo variando la
fase
![]() .
.
Grating Lobes
Come
abbiamo visto
![]() è una funzione periodica di periodo
è una funzione periodica di periodo
![]() essa
ha N poli pari al numero degli elementi radianti, al variare di N si
può verificare l'insorgenza di lobi laterali dannosi per la
direttività dell'antenna; ad esempio il caso radar è
lampante: possono esserci lobi laterali che irradiano in direzioni
non volute catturando del clutter, un segnale indesiderato che si
sovrappone al segnale utile rendendo difficile il riconoscimento di
quest'ultimo.
essa
ha N poli pari al numero degli elementi radianti, al variare di N si
può verificare l'insorgenza di lobi laterali dannosi per la
direttività dell'antenna; ad esempio il caso radar è
lampante: possono esserci lobi laterali che irradiano in direzioni
non volute catturando del clutter, un segnale indesiderato che si
sovrappone al segnale utile rendendo difficile il riconoscimento di
quest'ultimo.
Tenendo conto che:
![]() e
e
![]() considerando
considerando
![]() quindi
un angolo polare ne segue che:
quindi
un angolo polare ne segue che:
![]()
occorre:
![]() cioè che
cioè che
![]() sia
al massimo il valore dell'ultimo zero prima di riavere un lobo
maggiore in modo da avere dei lobi laterali i più piccoli
possibili.
sia
al massimo il valore dell'ultimo zero prima di riavere un lobo
maggiore in modo da avere dei lobi laterali i più piccoli
possibili.
Quindi:
![]()
e
![]()
otteniamo la seguente espressione generale per la lunghezza tra i dipoli normalizzata alla lunghezza d'onda:
![]()
esempio
nel caso broadside
![]() con
N molto grande:
con
N molto grande:
![]()
nel
caso endfire e backfire
![]() o
o
![]() :
:
![]()
in generale l'esperienza ha dimostrato che tale distanza non deve essere troppo grande.
Queste antenne hanno diversi campi di applicazione, come detto una delle sue applicazioni è nel caso radar. Ad esempio per scandire una certa regione di spazio variando la fase delle alimentazioni, in modo da variare progressivamente l'angolo di scansione:
![]()
![]()
in modo da rivelare o meno la presenza di un aereo, quindi antenna per Radar ATC.
Un altro caso sempre nel caso di applicazione radar è il caso del Radar ad apertura sintetica, SAR, usato per il telerilevamento di immagini fisse da satellite. La posizione dei singoli dipoli può essere quella di una singola antenna montata a bordo del satellite, che emette impulsi ad esempio a banda larga in istanti successivi di tempo per effettuare un mappaggio del terreno ad alta risoluzione dato che il sistema di antenne che così si viene a costruire genera un fascio molto stretto come abbiamo visto dai diagrammi di radiazione soprariportati.
Per parlare della propagazione è utile prendere in considerazione la seguente figura relativa ai vari strati dell'atmosfera:
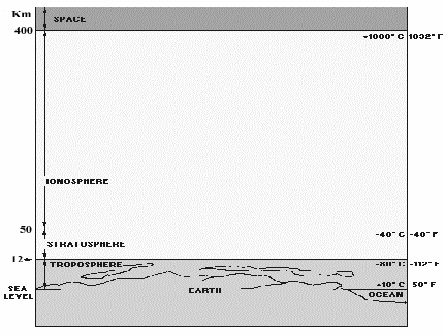
come si vede essa è costituita fondamentalmente da tre strati principali, di cui l'ultiomo può essere visto ancora come un insieme di strati, essi sono:
Troposfera: lo strato più basso che si estende dal livello del marte fino a una decina di Km
Stratosfera: che si estende dalla troposfera fino a 50 km
Ionosfera: lo strato più esterno che si estende da 50 fino a 400km sul livello del mare. Deve il suo nome al fatto che il sole incidendo su questo strato genera un gran numero di ioni, per il fatto che toglie elettroni agli atomi che lo compongono. E' uno strato molto importante per le comunicazioni radio.
La propagazione del segnale può avvenire in diversi modi, ma fopndamentemente abbiamo i seguenti casi:
Onda di superficie: è il caso in cui l'onda per diffrazione segue la curvatura della terra. Dalla teoria delle onde sappiamo che questo fenomeno è rilevante quando le strutture che incontra l'onda sono paragonabile alla lunghezza d'onda della stessa; le microonde e le onde corte non risentono quindi di questo fenomeno, mentre le onde medie e lunghe ne risentono fortemente. Nella seguente figura vediamo questo fenomeno di propagazione:
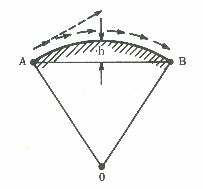
Esso
è importante quindi quando la distanza h proporzionale alla
curvatura della terra diviene elevata. Quando la distanza è
1000km essa è di 31km e le onde medie e lòunghe
cominciano a risentirne(![]() ).
).
Onda diretta e riflessa:è il caso molto frequente delle microonde, in cui esiste un cammino diretto o riflesso o entrambi tra l'antenna trasmittente e ricevente.
Onda spaziale: è il caso della propagazione ionosferica, tra l'antenna trasmittente e ricevente possono esserci distanze grandissime per il fatto che l'onda riflessa dalla ionosfera rimbalza sulla terra anche più volte coprendo in tal modo distanze elevatissime.
Nella seguente figura possiamo vedere nell'insieme questi fenomeni di propagazione:
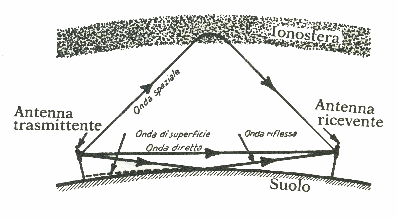
Propagazione per onda diretta e riflessa
Un caso molto importante come detto è il caso in cui esiste un cammino in linea di vista (LOS; line of sight) tra antenna trasmittente e ricevente. E' il caso dei ponti radio. La distanza tra questi non deve essere poi molto elevata, perchè come sappiamo irradiando l'antenna un onda sferica essa decade come 1/distanza e a grandi distanze tale fattore di attenuazione può essere molto grande. Come abbiamo visto nella pratica l'antenna può avere un diagramma di radiazione anche con alcuni lobi laterali(1 o più). Questi lobi laterali irradiando un campo possono generare un campo abbastanza intenso che riflettendo su un qualche materiale, ad esempio il terreno arrivano all'antenna ricevente in un tempo successivo a quello irradiato dal lobo principale. Se facessimo riferimento alla risposta impulsiva del canale trasmissivo tempo-invariante, avremmo:
![]()
dove
![]() è
una certa attenuazione sul cammino riflesso e
è
una certa attenuazione sul cammino riflesso e
![]() invece è il ritardo del raggio riflesso stesso. La sua
trasformata sarebbe:
invece è il ritardo del raggio riflesso stesso. La sua
trasformata sarebbe:
![]()
dalla teoria dei segnali sappiamo che un segnale non viene distorto qualora il segnale ricevuto:
![]()
ove k è una costante moltiplicativa e t0 un certo ritardo. Quindi dovremmo avere:
![]()
Come
si vede però
![]() per
il caso preso in esame non è costante in frequenza, almeno
nella banda del segnale, e con fase lineare. Se però
per
il caso preso in esame non è costante in frequenza, almeno
nella banda del segnale, e con fase lineare. Se però
![]() fosse
piccolo potremmo sviluppare l'esponenziale in serie ed avere in
questo caso un comportamento abbastanza lineare. In pratica però
abbiamo distorsioni sia di ampiezza che di fase. Sul segnale questo
si traduce ad avere in ricezione un replica del segnale di partenza
più repliche sia simmetriche(distorsioni di ampiezza) che
antisimmetriche (distorsioni di fase) rispetto alla replica centrale.
Questo potremmo vederlo sviluppando H(f) in serie di Taylor,
riconosceremmo un certo t0 attorno al quale ci sono queste repliche.
Questo fenomeno si chiama dispersione del segnale; è un
fenomeno molto sentito nel caso di trasmissione numerica a larga
banda; gli impulsi inviati su questo canale verrebbero allargati in
ricezione con conseguenti problemi del ricevitore a distinguere tali
impulsi e quindi insorgerebbero dei problemi di prestazioni. Tali
prestazioni come sappiamo sono la probabilità di errore e la
potenza di segnale minima ricevuta.
fosse
piccolo potremmo sviluppare l'esponenziale in serie ed avere in
questo caso un comportamento abbastanza lineare. In pratica però
abbiamo distorsioni sia di ampiezza che di fase. Sul segnale questo
si traduce ad avere in ricezione un replica del segnale di partenza
più repliche sia simmetriche(distorsioni di ampiezza) che
antisimmetriche (distorsioni di fase) rispetto alla replica centrale.
Questo potremmo vederlo sviluppando H(f) in serie di Taylor,
riconosceremmo un certo t0 attorno al quale ci sono queste repliche.
Questo fenomeno si chiama dispersione del segnale; è un
fenomeno molto sentito nel caso di trasmissione numerica a larga
banda; gli impulsi inviati su questo canale verrebbero allargati in
ricezione con conseguenti problemi del ricevitore a distinguere tali
impulsi e quindi insorgerebbero dei problemi di prestazioni. Tali
prestazioni come sappiamo sono la probabilità di errore e la
potenza di segnale minima ricevuta.
Tale fenomeno comunque si presenta molto spesso anche per diversi altri effetti che abbiamo sui canali trasmissivi. Ad esempio se il mezzo è dispersivo, ovvero quando la costante di propagazione dipende dalla frequenza, oppure nel caso multipath, cioè quando abbiamo moltissimoi cammini, non solo uno solo riflesso.
Il caso di mezzo dispersivo è quello del plasma(ionosfera) ma ci sono anche altri matreriale a presentare questo fenomeno, ad esempio metalli. Il problema nasce dal fatto che la velocità di fase:
![]()
dipende
da
![]() in
quanto la permettività dielettrica dipende da
in
quanto la permettività dielettrica dipende da
![]() cioè
dalla frequenza.
cioè
dalla frequenza.
Un
segnale inviato da un'antenna è un segnale in genere non
monofrequenziale(caso raro esempio notturno per le stazioni
radiofoniche) ma ha una certa banda seppur stretta attorno a una
certa frequenza. Ogni componente di questo segnale viaggia per quanto
dice la formula a velocità diversa e quindi si ricombina in
ricezione con differenti ritardi; per quanto detto nel caso multipath
abbiamo dispersione e quindi lo stesso fenomeno accade in questo
caso. Questo significa quindi che il segnale in ricezione è
non solo allargato ma anche distorto in qualche misura; se non vi
sono perdite il fenomeno che abbiamo è un allargamento
dell'impulso e un suo abbassamento(l'energia deve rimanere costante
in assenza di perdite) e quindi appunto distorsione, abbiamo anche un
fenomeno di slittamento tra portante ed inviluppo che non da luogo in
questo caso a distorsioni apprezzabili. Il fenomeno può essere
mitigato cercando di rendere il segnale tanto più a banda
stretta e diminuendo la distanza tra trasmettitore e ricevitore.
Sviluppando infatti in serie di Taylor la frequenza dell'onda
trasmessa otteniamo un segnale portante modulato da un certo
inviluppo la cui altezza decade come
![]() ove
t è il tempo; come si vede il fenomeno è tanto più
marcato quanto più il tempo di propagazione tra le due antenne
è maggiore.
ove
t è il tempo; come si vede il fenomeno è tanto più
marcato quanto più il tempo di propagazione tra le due antenne
è maggiore.
Vediamo ora di quantificare il fenomeno nei ponti radio:
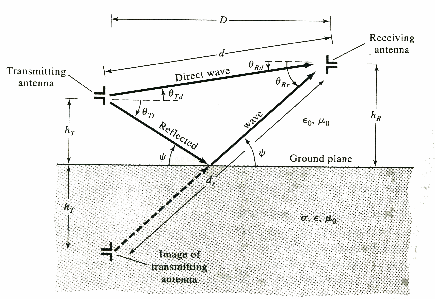
Per il principio delle immagini se l'antenna è posta verticalmente, possiamo assimilare l'onda riflessa come quella generata da un'antenna posta sotto il piano di massa che eroghi un campo uguale a quello trasmesso dall'antenna vera.
Segnale
diretto:
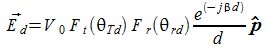
Segnale
riflesso:
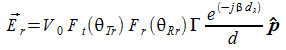
con
ovvia notazione dei simboli, con
![]() coefficiente di riflessione del terreno e Ft ed Fr i pattern delle
due antenne.
coefficiente di riflessione del terreno e Ft ed Fr i pattern delle
due antenne.
Il campo totale è quindi:

per
il coefficiente di riflessione, si ha che per piccoli angoli di
grazing(l'angolo
![]() in
figura) questo tende a valere -1. Inoltre d dr hanno lo stesso ordine
di grandezza, quindi il termine F della formula di cui sopra vale:
in
figura) questo tende a valere -1. Inoltre d dr hanno lo stesso ordine
di grandezza, quindi il termine F della formula di cui sopra vale:
![]() ove
ove
![]()
quindi prendendo il modulo del campo abbiamo:
![]()
![]()
se
esprimiamo questo fattore in funzione dell'altezza delle singole
antenne e facciamo tendere
![]() a
zero otteniamo:
a
zero otteniamo:
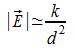
ove
k è una certa costante. Otteniamo quindi un campo che decade
come
![]() non inversamente a d come nel caso della propagazione diretta. Quindi
in questo caso la potenza decade molto più velocemente del
caso con sola onda diretta in particolare proporzionalmente
all'inverso della quarta potenza della distanza.
non inversamente a d come nel caso della propagazione diretta. Quindi
in questo caso la potenza decade molto più velocemente del
caso con sola onda diretta in particolare proporzionalmente
all'inverso della quarta potenza della distanza.
Propagazione Multipath
In molti casi non si ha nemmeno un cammino diretto. E' in caso non-LOS o NLOS. Ad esempio è il caso della comunicazione tra dispositivi radiomobili, GSM e UMTS, infatti in aria urbana il segnale può arrivare al ricevitore seguendo diversi percorsi; in pratica quindi il segnale è una sovrapposizione di tantissime repliche che arrivano con attenuazione e fase casuali. Nella figu7ra seguente sono riassunti i vari fenomeni di propagazione del canale NLOS:
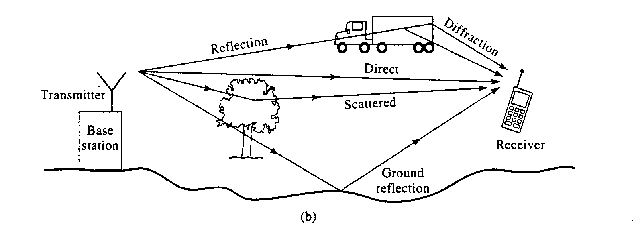
Il segnale inviato dall'antenna trasmittente è comunque sia un segnale passa banda centrato su una certa frequenza centrale, lo possiamo sintetizzare nella seguente espressione:
![]()
ove
![]() è
l'inviluppo complesso dello stesso. Un caso particolare è
quando s(t) è un semplice segnale sinusoidale
è
l'inviluppo complesso dello stesso. Un caso particolare è
quando s(t) è un semplice segnale sinusoidale
![]() e quindi
e quindi
![]()
Il segnale ricevuto in tal caso è:
![]()
posto:
![]() si ha:
si ha:
![]()
si
può dimostrare che l'ampiezza del segnale fluttua con densità
di probabilità data dalla densità di probabilità
di Rayleigh e la fase che varia molto velocemente fluttua con densità
di probabilità uniforme in![]() .
.
Infatti abbiamo:
![]()
per il teorema del limite centrale:
![]()
![]()
sono dei processi Gaussiani perchè somma di tante variabile aleatorie identicamente distribuite, nella pratica ampiezza e fase variano nel tempo per via che il canale non è stazionario.
Quindi abbiamo:
![]() è una variabile aleatoria di
Rayleigh,
è una variabile aleatoria di
Rayleigh,
![]()
![]() è
uniformemente distribuita in
è
uniformemente distribuita in![]()
questo fenomeno si chiama Fading, evanescenza, con queste due proprietà come possiamo vedere nella seguente figura:
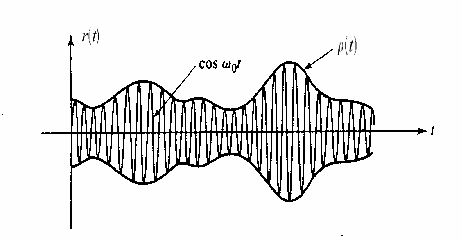
Il Fading fa si che le fluttuazioni del segnale siano parecchio veloci, e anche di diversi db tra un valore e all'altro dell'ampiezza del segnale ricevuto.
Per superare questo inconveniente su canale radiomobile sono adottate diverse tecniche, le più importanti delle quali sono quelle a spettro espanso; la banda del segnale da stretta che è viene espansa su un intervallo spettrale molto più grande, in tal modo essendo lo spettro fortemente espanso sono una piccola frazione di esso viene interessata dalla forma indesiderata che il canale in tali casi viene ad assumere e quindi non si manifestano delle grosse distorsioni nel segnale ricevuto. Come abbiamo visto le distorsioni più importanti che abbiamo sono quelle di ampiezza e fase. Nella pratica se la banda del segnale è dello stesso ordine di grandezza o vicina a quella del canale si manifesta come abbiamo visto il fenomeno della dispersione.
Altre tecniche usate in altre applicazioni sono quelle della diversità di spazio o frequenza. In particolare nella diversità di spazio, sapendo che il fading si manifesta come forti fluttuazioni tra un punto e un altro dello spazio usa una due antenne diverse poste in ricezione.
Propagazione ionosferica
Un altro caso interessante è quello della propagazione dell'onda spaziale. Il segnale inviato da terra colpisce gli strati più alti dell'atmosfera caratterizzati da alta ionizzazione e quindi basso indice di rifrazione e viene riflessa verso terra, dove incontrando la superficie imperfettamente conduttrice della stessa venendo riflessa nella ionosfera viene riflessa ancora verso terra e così via percorrendo distanze grandissime dal trasmettitore.
L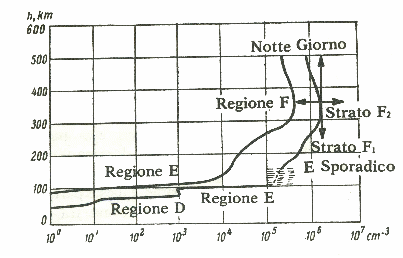
a
ionosfera è caratterizzata da diversi strati ionizzanti con
diversa densità di ionizzazione. Sperimentalmente si vede come
indica la seguente figura che questa densità di elettroni
aumenta progressivamente con l'altezza e poi a un certo punto
diminuisce:
in figura notiamo tre strati principale D, E, F a cui se ne aggiungono degli altri in diverse ore del giorno o in diverse stagioni. Ovviamente la ionizzazione sarà parecchio maggiore durante il giorno che di notte.
Per l'onda inviata abbiamo quindi la seguente situazione:

per angoli di incidenza abbastanza elevati(rispetto alla normale ai vari strati) l'onda viene riflessa, mentre per angoli minori c'è il rischio che l'onda sfugga oltre la ionosfera. Sperimentalmente si verifica anche che oltre 30MHZ l'onda non viene riflessa verso terra.
Il plasma, un generico strato della ionosfera è caratterizzato da una permeabilità elettrica del tipo:
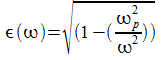
ove
![]() è
la pulsazione di lavoro e
è
la pulsazione di lavoro e
![]() è
la cosiddetta pulsazione di taglio del plasma e ha un valore che
dipende dalla densità degli elettroni. Se abbiamo un incidenza
perpendicolare possiamo avere due casi:
è
la cosiddetta pulsazione di taglio del plasma e ha un valore che
dipende dalla densità degli elettroni. Se abbiamo un incidenza
perpendicolare possiamo avere due casi:
![]()
![]() è
puramente immaginario, non si ha quindi propagazione
è
puramente immaginario, non si ha quindi propagazione
![]()
![]() è
reale e si ha propagazione
è
reale e si ha propagazione
questo
lo si vede dalla costante di propagazione![]() in
cui
in
cui
![]() rappresenta
il termine propagativo ed
rappresenta
il termine propagativo ed
![]() l'attenuazione.
Come si vede nel primo caso il termine
l'attenuazione.
Come si vede nel primo caso il termine![]() è
del tutto assente, il caso opposto è il secondo in cui è
è
del tutto assente, il caso opposto è il secondo in cui è
![]() ad
essere assente.
ad
essere assente.
Un caso interessante però è quello di incidenza obliqua; in tal caso come visto la propagazione dipende sia dalla frequenza ma anche dall'angolo di incidenza stesso.
Ammettendo
ad esempio di avere n0=1 per l'indice di rifrazione nella troposfera,
un caso abbastanza verosimile e
![]() l'angolo
di incidenza sul primo strato, il percorso dell'onda deve seguire la
legge di Schnell:
l'angolo
di incidenza sul primo strato, il percorso dell'onda deve seguire la
legge di Schnell:
![]()
essendo
l'indice di rifrazione in diminuzione con l'altezza, l'angolo di
uscita dell'onda da uno strato tende ad aumentare fino a che tale
angolo
![]() tende
a 90°, come si può vedere in figura:
tende
a 90°, come si può vedere in figura:
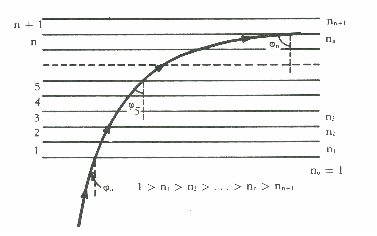
in tal caso abbiamo:
![]()
sostituendo l'espressione dell'indice di rifrazione dell'ennesimo strato si trova:
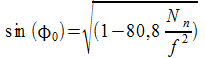
come si vede l'angolo di incidenza sul primo strato dipende dalla frequenza altrimenti non abbiamo riflessione.
Tale modo di comunicare a distanza è proprio dei radioamatori, in cui si usano frequenze al di sotto dei 30MHZ riuscendo a copriore distanze elevatissime dall'apparato trasmittente.
C'è però un problema con questo tipo di comunicazioni. Essendo riflesso dalla ionosfera il segnale prima di giungere a terra deve percorrere una distanza abbastanza elevata: la cosiddetta distanza skip, quindi un'eventuale antenna posta prima di questa distanza potrebbe non captare alcun segnale. Nella pratica l'antenna trasmittente per esempio per onde lunghe, potrebbe inviare anche un'onda di superfice che come abbiamo visto per diffrazione non può raggiungere distanze molto elevate massimo 3000km, quindi c'è una zona cosidetta zona skip o di silenzio radio in cui non è alcuno dei due segnali di cui abbiamo parlato, onda spaziale e di superficie, lo possiamo vedere nella seguente figura:
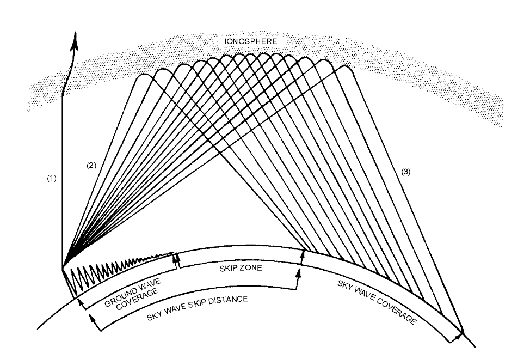
Questo fenomeno è abbastanza sentito nelle onde lunghe e medie dove vi sono ambedue i tipi di segnali. Nelle onde corte invece il modo di propagarsi delle onde è principalmente quello spaziale.
Nelle
onde medie e lunghe![]() oltretutto il segnale deve propagarsi in profondità nella
ionosfera prima di essere ri8flesso e questo da luogo a grandi
attenuazioni. Nel caso delle onde corte
oltretutto il segnale deve propagarsi in profondità nella
ionosfera prima di essere ri8flesso e questo da luogo a grandi
attenuazioni. Nel caso delle onde corte
![]() esse vengono riflesse immediatamente e l'attenuazione è
praticamente irrilevante.
esse vengono riflesse immediatamente e l'attenuazione è
praticamente irrilevante.